| Title | Asymptotic quantization error of continuous signals and the quantization dimension |
| Publication Type | Journal Article |
| Year of Publication | 1982 |
| Authors | Paul L. Zador |
| Journal | IEEE Trans. Inform. Theory |
| Volume | IT-28 |
| Pagination | 139–149 |
| Date Published | March |
| Keywords | information-theory, nldr, rate-distortion, source-coding, vector-quantization |
| Abstract | Extensions of the limiting quantization error formula of Bennet are proved. These are of the form |

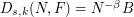 , where
, where 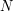 is the number of output levels,
is the number of output levels, 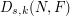 is the
is the  th moment of the metric distance between quantizer input and output,
th moment of the metric distance between quantizer input and output, 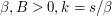 is the signal space dimension, and
is the signal space dimension, and 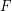 is the signal distribution. If a suitably well-behaved
is the signal distribution. If a suitably well-behaved 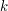 -dimensional signal density
-dimensional signal density 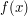 exists,
exists, ![$ B=b_{s,k}[\int f^{rho}(x)dx]^{1/ rho},rho=k/(s+k) $](/sites/default/files/tex/6647d3d19b1bd6a9fb01f5d61b66406818fb9d3b.png) , and
, and 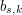 does not depend on
does not depend on 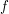 . For
. For 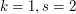 this reduces to Bennett's formula. If
this reduces to Bennett's formula. If ![$ [0,1] $](/sites/default/files/tex/5fcfff9519d875b0685a39d44bcf1351fae82f92.png) ,
, 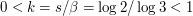 and this
and this ![$ [12,13] $](/sites/default/files/tex/f98bc98c6de6ee7756c1e956667f6cbe9a5958df.png) . Random quantization, optimal quantization in the presence of an output information constraint, and quantization noise in high dimensional spaces are also investigated.
. Random quantization, optimal quantization in the presence of an output information constraint, and quantization noise in high dimensional spaces are also investigated.