| Title | A space quantization method for numerical integration |
| Publication Type | Journal Article |
| Year of Publication | 1998 |
| Authors | Gilles Pagès |
| Journal | J. Comput. Appl. Math. |
| Volume | 89 |
| Pagination | 1–38 |
| ISSN | 0377-0427 |
| Keywords | competitive algorithms, error estimation, learning algorithms, numerical integration, numerical methods, optimization method, vector quantization, Voronoi diagram |
| Abstract | We propose a new method (SQM) for numerical integration of |

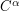 functions (
functions (![$ \alpha \in (0,2] $](/sites/default/files/tex/47d5ea2082fb384bf7d64a87a2c115701b9507e4.png) ) defined on a convex subset
) defined on a convex subset 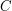 of
of 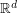 with respect to a continuous distribution
with respect to a continuous distribution 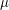 . It relies on a space quantization of
. It relies on a space quantization of  -tuple
-tuple 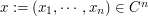 .
. 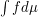 is approximated by a weighted sum of the
is approximated by a weighted sum of the 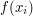 's. The integration error bound depends on the distortion
's. The integration error bound depends on the distortion 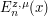 of the Voronoï tessellation of
of the Voronoï tessellation of  . This notion comes from Information Theoretists. Its main properties (existence of a minimizing
. This notion comes from Information Theoretists. Its main properties (existence of a minimizing 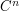 , asymptotics of
, asymptotics of 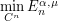 as
as 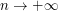 ) are presented for a wide class of measures
) are presented for a wide class of measures 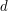 ,
, 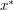 and the characteristics of its Voronoï tessellation. Some new results on the Competitive Learning Vector Quantization algorithm (when
and the characteristics of its Voronoï tessellation. Some new results on the Competitive Learning Vector Quantization algorithm (when 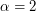 ) are obtained as a by-product. Some tests, simulations and provisional remarks are proposed as a conclusion.
) are obtained as a by-product. Some tests, simulations and provisional remarks are proposed as a conclusion.