| Title | Local distortion and µ-mass of the cells of one dimensional asymptotically optimal quantizers |
| Publication Type | Journal Article |
| Year of Publication | 2004 |
| Authors | Sylvain Delattre, Jean-Claude Fort, and Gilles Pagès |
| Journal | Communications in Statistics. Theory and Methods |
| Volume | 33(5) |
| Start Page | 1087-1117 |
| Date Published | 2004 |
| Abstract | We consider one dimensional probability distributions |

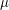 having a continuous and positive probability density function. We find the asymptotic of the size and the mass of the Voronoi cells and we prove that the local distortion associated with stationary or optimal quantizers is asymptotically uniform. Numerical simulations and computations illustrate the theoretical results and lead to the design of some good-fit test for the stationary equilibria.
having a continuous and positive probability density function. We find the asymptotic of the size and the mass of the Voronoi cells and we prove that the local distortion associated with stationary or optimal quantizers is asymptotically uniform. Numerical simulations and computations illustrate the theoretical results and lead to the design of some good-fit test for the stationary equilibria.