| Title | Quantization of probability distributions under norm-based distortion measures |
| Publication Type | Journal Article |
| Year of Publication | 2004 |
| Authors | Sylvain Delattre, Siegfried Graf, Harald Luschgy, and Gilles Pagès |
| Keywords | empirical measure, High-rate vector quantization, local distortion, norm-difference distortion, Point density measure, weak convergence |
| Abstract | For a probability measure |
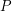 on
on 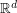 and
and 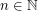 consider
consider 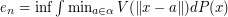 where the infimum is taken over all subsets
where the infimum is taken over all subsets  of
of 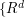 with
with 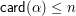 and
and 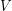 is a nondecreasing function. Under certain conditions on
is a nondecreasing function. Under certain conditions on 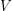 , we derive the precise
, we derive the precise  -asymptotics of
-asymptotics of 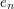 for nonsingular and for (singular) self-similar distributions
for nonsingular and for (singular) self-similar distributions 