| Abstract | Optimal quantization has been recently revisited in multi-dimensional numerical integration (see [1]), multi-asset American option pricing (see [2]), control theory (see [3]) and nonlinear filtering theory (see [4]). In this paper, we enlighten some numerical procedures in order to get some accurate optimal quadratic quantization of the Gaussian distribution in one and higher dimensions. We study in particular Newton method in the deterministic case (dimension 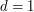 ) and stochastic gradient in higher dimensional case ( ) and stochastic gradient in higher dimensional case (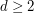 ). Some heuristics are provided which concern the step in the stochastic gradient method. Finally numerical examples borrowed from mathematical finance are used to test the accuracy of our Gaussian optimal quantizers. ). Some heuristics are provided which concern the step in the stochastic gradient method. Finally numerical examples borrowed from mathematical finance are used to test the accuracy of our Gaussian optimal quantizers.
References- Gilles Pagès,
"A space quantization method for numerical integration",
J. Comput. Appl. Math., vol. 89, no. 1, Amsterdam, The Netherlands, Elsevier Science Publishers B. V., pp. 1–38, 1998.
- Vlad Bally, Gilles Pagès, and Jacques Printems,
"A stochastic quantization method for nonlinear problems",
Monte Carlo Methods and Applications, vol. 7(1), pp. 21-34, 2001.
- Gilles Pagès, Huyên Pham, and Jacques Printems,
"An optimal Markovian quantization algorithm for multidimensional stochastic control problems",
Stochastics and Dynamics, vol. 4(4), pp. 501-545, 2004.
- Gilles Pagès, and Huyên Pham,
"Optimal quantization methods for nonlinear filtering with discrete-time observations",
Bernoulli, vol. 11(5), 2005.
|