| Title | Error analysis of the quantization algorithm for obstacle problems |
| Publication Type | Journal Article |
| Year of Publication | 2003 |
| Authors | Vlad Bally, and Gilles Pagès |
| Journal | Stochastic Processes & Their Applications |
| Volume | 106(1) |
| Start Page | 1-40 |
| Keywords | American option pricing, Numerical Probability, Optimal Stopping, Quantization of random variables, Reflected Backward Stochastic Differential Equation, Snell envelope |
| Abstract | In the accompanying paper [2] an algorithm based on a "quantized tree" is designed to compute the solution of multi-dimensional obstacle problems for homogeneous |
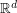 -valued Markov chains. It is based on the quantization of probability distributions which yields a dynamic programming formula on a discrete tree. A typical example of such problems is the pricing of multi-asset American style vanilla options. In the first part of the present paper, the analysis of the
-valued Markov chains. It is based on the quantization of probability distributions which yields a dynamic programming formula on a discrete tree. A typical example of such problems is the pricing of multi-asset American style vanilla options. In the first part of the present paper, the analysis of the 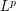 -error is completed. In the second part, we estimate the error induced by the Monte Carlo estimation of the transition weights involved in the (optimal) quantized tree.
-error is completed. In the second part, we estimate the error induced by the Monte Carlo estimation of the transition weights involved in the (optimal) quantized tree.