A new grid method for computing the Snell envelope of a function of an 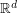 -valued simulatable Markov chain -valued simulatable Markov chain 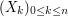 is proposed. (This is a typical nonlinear problem that cannot be solved by the standard Monte Carlo method.) Every is proposed. (This is a typical nonlinear problem that cannot be solved by the standard Monte Carlo method.) Every 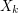 is replaced by a 'quantized approximation' is replaced by a 'quantized approximation' 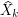 taking its values in a grid taking its values in a grid 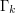 of size of size 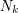 . The . The  grids and their transition probability matrices form a discrete tree on which a pseudo-Snell envelope is devised by mimicking the regular dynamic programming formula. Using the quantization theory of random vectors, we show the existence of a set of optimal grids, given the total number grids and their transition probability matrices form a discrete tree on which a pseudo-Snell envelope is devised by mimicking the regular dynamic programming formula. Using the quantization theory of random vectors, we show the existence of a set of optimal grids, given the total number 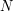 of elementary of elementary 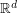 -valued quantizers. A recursive stochastic gradient algorithm, based on simulations of ( -valued quantizers. A recursive stochastic gradient algorithm, based on simulations of (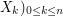 , yields these optimal grids and their transition probability matrices. Some a priori error estimates based on the , yields these optimal grids and their transition probability matrices. Some a priori error estimates based on the 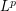 -quantization errors -quantization errors 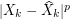 are established. These results are applied to the computation of the Snell envelope of a diffusion approximated by its (Gaussian) Euler scheme. We apply these results to provide a discretization scheme for reflected backward stochastic differential equations. Finally, a numerical experiment is carried out on a two-dimensional American option pricing problem. are established. These results are applied to the computation of the Snell envelope of a diffusion approximated by its (Gaussian) Euler scheme. We apply these results to provide a discretization scheme for reflected backward stochastic differential equations. Finally, a numerical experiment is carried out on a two-dimensional American option pricing problem. | 
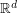 -valued simulatable Markov chain
-valued simulatable Markov chain 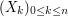 is proposed. (This is a typical nonlinear problem that cannot be solved by the standard Monte Carlo method.) Every
is proposed. (This is a typical nonlinear problem that cannot be solved by the standard Monte Carlo method.) Every 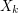 is replaced by a 'quantized approximation'
is replaced by a 'quantized approximation' 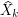 taking its values in a grid
taking its values in a grid 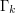 of size
of size 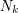 . The
. The  grids and their transition probability matrices form a discrete tree on which a pseudo-Snell envelope is devised by mimicking the regular dynamic programming formula. Using the quantization theory of random vectors, we show the existence of a set of optimal grids, given the total number
grids and their transition probability matrices form a discrete tree on which a pseudo-Snell envelope is devised by mimicking the regular dynamic programming formula. Using the quantization theory of random vectors, we show the existence of a set of optimal grids, given the total number 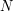 of elementary
of elementary 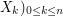 , yields these optimal grids and their transition probability matrices. Some a priori error estimates based on the
, yields these optimal grids and their transition probability matrices. Some a priori error estimates based on the 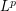 -quantization errors
-quantization errors 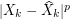 are established. These results are applied to the computation of the Snell envelope of a diffusion approximated by its (Gaussian) Euler scheme. We apply these results to provide a discretization scheme for reflected backward stochastic differential equations. Finally, a numerical experiment is carried out on a two-dimensional American option pricing problem.
are established. These results are applied to the computation of the Snell envelope of a diffusion approximated by its (Gaussian) Euler scheme. We apply these results to provide a discretization scheme for reflected backward stochastic differential equations. Finally, a numerical experiment is carried out on a two-dimensional American option pricing problem.