| Title | Construction of optimal quantizers for Gaussian measures on Banach spaces |
| Publication Type | Thesis |
| Year of Publication | 2008 |
| Authors | Benedikt Wilbertz |
| Advisor | Harald Luschgy |
| Academic Department | Mathematik |
| University | Universität Trier |
| Keywords | approximation, Banach space, Brownian motion, Gaussian measures, quantization |
| Abstract | In this thesis, we investigate the quantization problem of Gaussian measures on Banach spaces by means of constructive methods. |
| Native Abstract | In dieser Arbeit untersuchen wir das Quantisierungsproblem für Gaußmaße auf Banachräumen mit Hilfe von konstruktiven Verfahren. |
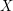 and a natural number
and a natural number 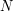 , we are searching for those
, we are searching for those ![$ [0,1] $](/sites/default/files/tex/5fcfff9519d875b0685a39d44bcf1351fae82f92.png) equipped with the supremum-norm, since in that case all known methods failed to achieve the optimal quantization rate for important Gauss-processes.
equipped with the supremum-norm, since in that case all known methods failed to achieve the optimal quantization rate for important Gauss-processes. -width we were able to attain the optimal rate of convergence to zero for these quantization problems.
-width we were able to attain the optimal rate of convergence to zero for these quantization problems.