Home » Publications

Fractal functional quantization of mean-regular stochastic processes

TitleFractal functional quantization of mean-regular stochastic processes
Publication TypeJournal Article
Year of Publication2010
AuthorsHarald Luschgy, Siegfried Graf, and Gilles Pagès
JournalMathematical Proceedings of the Cambridge Philosophical Society
Abstract

We investigate the functional quantization problem for stochastic processes with respect to 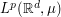$ L^p(\mathbb{R}^d, \mu) $-norms, where 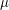$ \mu $ is a fractal measure namely, $ \mu $ is self-similar or a homogeneous Cantor measure. The derived functional quantization upper rate bounds are universal depending only on the mean-regularity index of the process and the quantization dimension of $ \mu $ and as universal rates they are optimal. Furthermore, for arbitrary Borel probability measures $ \mu $ we establish a (nonconstructive) link between the quantization errors of $ \mu $ and the functional quantization errors of the process in the space $ L^p(\mathbb{R}^d, \mu) $.