| Title | Quantization for probability measures in the Prokhorov metric |
| Publication Type | Journal Article |
| Year of Publication | 2009 |
| Authors | Harald Luschgy, and Siegfried Graf |
| Journal | Theory Probab. Appl. |
| Volume | 53 |
| Pagination | 216-241 |
| Keywords | asymptotic quantization error, empirical measures, entropy, Ky Fan metric, multidimensional quantization, optimal quantizers, Prokhorov metric, quantization dimension |
| Abstract | For a probability distribution |

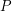 on
on 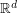 and
and 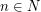 consider
consider 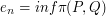 , where
, where  denotes the Prokhorov metric and the infimum is taken over all discrete probabilities
denotes the Prokhorov metric and the infimum is taken over all discrete probabilities 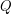 with
with 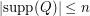 . We study solutions
. We study solutions  th quantization error en as
th quantization error en as 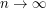 .
. 