| Title | Small ball probabilities around random centers of Gaussian measures and applications to quantization |
| Publication Type | Journal Article |
| Year of Publication | 2003 |
| Authors | Steffen Dereich |
| Journal | J. Theor. Probab. |
| Volume | 16(2) |
| Pagination | 427-449 |
| Keywords | Gaussian process, quantization, small ball probabilites for random centers |
| Abstract | Let |

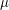 be a centered Gaussian measure on a separable Hilbert space
be a centered Gaussian measure on a separable Hilbert space 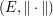 . We are concerned with the logarithmic small ball probabilities around a
. We are concerned with the logarithmic small ball probabilities around a 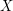 . It turns out that the asymptotic behavior of
. It turns out that the asymptotic behavior of 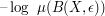 is a.s. equivalent to that of a deterministic function
is a.s. equivalent to that of a deterministic function 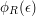 . These new insights will be used to derive the precise asymptotics of a random quantization problem which was introduced in a former article by Dereich, Fehringer, Matoussi, and Scheutzow [8].
. These new insights will be used to derive the precise asymptotics of a random quantization problem which was introduced in a former article by Dereich, Fehringer, Matoussi, and Scheutzow [8].