Home ยป Publications

On the link between small ball probabilities and the quantization problem for Gaussian measures on Banach spaces

TitleOn the link between small ball probabilities and the quantization problem for Gaussian measures on Banach spaces
Publication TypeJournal Article
Year of Publication2003
AuthorsSteffen Dereich, F. Fehringer, A. Matoussi, and M. Scheutzow
JournalJournal of Theoretical Probability
Volume16(1)
KeywordsGaussian process, High-resolution quantization, isoperimetric inequality., small ball probability
Abstract

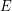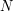Let m be a centered Gaussian measure on a separable Banach space $ E $ and $ N $ a positive integer. We study the asymptotics as 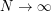$ N \to \infty $ of the quantization error, i.e., the infimum over all subsets $ \varepsilon $ of $ E $ of cardinality $ N $ of the average distance w.r.t. $ m $ to the closest point in the set $ \varepsilon $. We compare the quantization error with the average distance which is obtained when the set $ E $ is chosen by taking $ N $ i.i.d. copies of random elements with law $ m $. Our approach is based on the study of the asymptotics of the measure of a small ball around $ 0 $. Under slight conditions on the regular variation of the small ball function, we get upper and lower bounds of the deterministic and random quantization error and are able to show that both are of the same order. Our conditions are typically satisfied in case the Banach space is infinite dimensional.