| Title | Linear transformations and the k-means clustering algorithm: applications to clustering curves |
| Publication Type | Journal Article |
| Year of Publication | 2007 |
| Authors | Thaddeus Tarpey |
| Journal | Am Stat. |
| Volume | 61(1) |
| Pagination | 34–40 |
| Abstract | Functional data can be clustered by plugging estimated regression coefficients from individual curves into the k-means algorithm. Clustering results can differ depending on how the curves are fit to the data. Estimating curves using different sets of basis functions corresponds to different linear transformations of the data. k-means clustering is not invariant to linear transformations of the data. The optimal linear transformation for clustering will stretch the distribution so that the primary direction of variability aligns with actual differences in the clusters. It is shown that clustering the raw data will often give results similar to clustering regression coefficients obtained using an orthogonal design matrix. Clustering functional data using an |

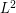 metric on function space can be achieved by clustering a suitable linear transformation of the regression coefficients. An example where depressed individuals are treated with an antidepressant is used for illustration.
metric on function space can be achieved by clustering a suitable linear transformation of the regression coefficients. An example where depressed individuals are treated with an antidepressant is used for illustration.