| Title | Universal $L^s$-rate-optimality of $L^r$-optimal quantizers by dilatation and contraction |
| Publication Type | Journal Article |
| Year of Publication | 2009 |
| Authors | Abass Sagna |
| Journal | ESAIM: Probability and Statistics |
| Volume | 13 |
| Pagination | 218-246 |
| Keywords | dilatation, empirical measure theorem, Lloyd algorithm, rate-optimal quantizers |
| Abstract | We investigate in this paper the properties of some dilatations or contractions of a sequence |

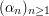 of
of 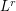 -optimal quantizers of an
-optimal quantizers of an 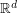 -valued random vector
-valued random vector 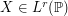 defined in the probability space
defined in the probability space 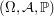 with distribution
with distribution 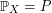 . To be precise, we investigate the
. To be precise, we investigate the 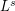 -quantization rate of sequences
-quantization rate of sequences 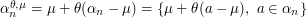 when
when 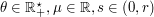 or
or 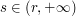 and
and 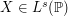 . We show that for a wide family of distributions, one may always find parameters
. We show that for a wide family of distributions, one may always find parameters 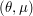 such that
such that 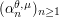 is
is 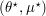 such that
such that 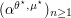 also satisfies the so-called
also satisfies the so-called 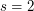 ,
, 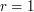 ) for the exponential distribution.
) for the exponential distribution. 