We develop a new approach to vector quantization, which guarantees an intrinsic stationarity property that also holds, in contrast to regular quantization, for non-optimal quantization grids. This goal is achieved by replacing the usual nearest neighbor projection operator for Voronoi quantization by a random splitting operator, which maps the random source to the vertices of a triangle of 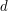 -simplex. In the quadratic Euclidean case, it is shown that these triangles or -simplex. In the quadratic Euclidean case, it is shown that these triangles or 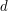 -simplices make up a Delaunay triangulation of the underlying grid. Furthermore, we prove the existence of an optimal grid for this Delaunay -- or dual -- quantization procedure. We also provide a stochastic optimization method to compute such optimal grids, here for higher dimensional uniform and normal distributions. A crucial feature of this new approach is the fact that it automatically leads to a second order quadrature formula for computing expectations, regardless of the optimality of the underlying grid. -simplices make up a Delaunay triangulation of the underlying grid. Furthermore, we prove the existence of an optimal grid for this Delaunay -- or dual -- quantization procedure. We also provide a stochastic optimization method to compute such optimal grids, here for higher dimensional uniform and normal distributions. A crucial feature of this new approach is the fact that it automatically leads to a second order quadrature formula for computing expectations, regardless of the optimality of the underlying grid. | 
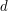 -simplex. In the quadratic Euclidean case, it is shown that these triangles or
-simplex. In the quadratic Euclidean case, it is shown that these triangles or 