In this paper, we investigate a method based on risk minimization to hedge observable but non-tradable source of risk on financial or energy markets. The optimal portfolio strategy is obtained by minimizing dynamically the Conditional Value-at-Risk (CVaR) using three main tools: stochastic approximation algorithm, optimal quantization and variance reduction techniques (importance sampling (IS) and linear control variable (LCV)) as the quantities of interest are naturally related to rare events. As a first step, we investigate the problem of CVaR regression, which corresponds to a static portfolio strategy where the number of units of each tradable assets is fixed at time 0 and remains unchanged till time 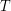 . 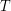We devise a stochastic approximation algorithm and study its a.s. convergence and rate of convergence. Then, we extend to the dynamic case under the assumption that the process modelling the non-tradable source of risk and financial assets prices are Markov. Finally, we illustrate our approach by considering several portfolios in the incomplete energy market. | 
