In this article, we develop a new approach to functional quantization, which consists in discretizing only the first Karhunen-Loève coordinates of a continuous Gaussian semimartingale 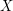 . Using filtration enlargement techniques, we prove that the conditional distribution of . Using filtration enlargement techniques, we prove that the conditional distribution of 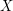 knowing its first Karhunen-Loève coordinates is a Gaussian semimartingale with respect to its natural filtration. knowing its first Karhunen-Loève coordinates is a Gaussian semimartingale with respect to its natural filtration.
This allows to define the partial quantization of a solution of a stochastic differential equation with respect to 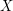 by simply plugging the partial functional quantization of by simply plugging the partial functional quantization of 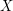 in the SDE. in the SDE.
Then, we provide an upper bound of the 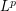 -partial quantization error for the solution of SDE involving the -partial quantization error for the solution of SDE involving the 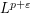 -partial quantization error for -partial quantization error for 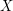 , for , for 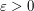 . The . The 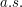 convergence is also investigated. convergence is also investigated.
Incidentally, we show that the conditional distribution of a Gaussian semimartingale 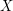 knowing that it stands in some given Voronoi cell of its functional quantization is a (non-Gaussian) semimartingale. As a consequence, the functional stratification method developed in [1], amounted in the case of solutions of SDE to use the Euler scheme of these SDE in each Voronoi cell. knowing that it stands in some given Voronoi cell of its functional quantization is a (non-Gaussian) semimartingale. As a consequence, the functional stratification method developed in [1], amounted in the case of solutions of SDE to use the Euler scheme of these SDE in each Voronoi cell.
References- Sylvain Corlay, and Gilles Pagès,
Functional quantization based stratified sampling methods,
, 2010.
| 
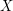 . Using filtration enlargement techniques, we prove that the conditional distribution of
. Using filtration enlargement techniques, we prove that the conditional distribution of 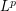 -partial quantization error for the solution of SDE involving the
-partial quantization error for the solution of SDE involving the 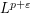 -partial quantization error for
-partial quantization error for 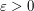 . The
. The 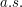 convergence is also investigated.
convergence is also investigated.