Quantization consists in studying the 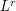 -error induced by the approximation of a random vector -error induced by the approximation of a random vector 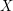 by a vector (quantized version) taking a finite number by a vector (quantized version) taking a finite number  of values. For of values. For 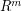 -valued random vectors the theory and practice is quite well established and in particular, the asymptotics as -valued random vectors the theory and practice is quite well established and in particular, the asymptotics as 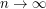 of the resulting minimal quantization error for nonsingular distributions is well known: it behaves like of the resulting minimal quantization error for nonsingular distributions is well known: it behaves like 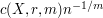 . This paper is a transposition of this problem to random vectors in an infinite dimensional Hilbert space and in particular, to stochastic processes . This paper is a transposition of this problem to random vectors in an infinite dimensional Hilbert space and in particular, to stochastic processes ![$ (X_t)_{t \in [0,1]} $](/sites/default/files/tex/98bd9f498338ce7efbb2ccf5f20055f0f356310b.png) viewed as viewed as ![$ L^2([0,1],dt) $](/sites/default/files/tex/97f973def8ab85a3be243077f6b2b87c2b850600.png) -valued random vectors. For Gaussian vectors and the -valued random vectors. For Gaussian vectors and the 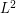 -error we present detailed results for stationary and optimal quantizers. We further establish a precise link between the rate problem and Shannon–Kolmogorov’s entropy of -error we present detailed results for stationary and optimal quantizers. We further establish a precise link between the rate problem and Shannon–Kolmogorov’s entropy of 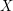 : This allows us to compute the exact rate of convergence to zero of the minimal : This allows us to compute the exact rate of convergence to zero of the minimal 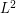 -quantization error under rather general conditions on the eigenvalues of the covariance operator. Typical rates are -quantization error under rather general conditions on the eigenvalues of the covariance operator. Typical rates are 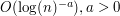 . They are obtained, for instance, for the fractional Brownian motion and the fractional Ornstein–Uhlenbeck process. The exponent a is closely related with the . They are obtained, for instance, for the fractional Brownian motion and the fractional Ornstein–Uhlenbeck process. The exponent a is closely related with the 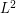 -regularity of the process. -regularity of the process. | 
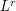 -error induced by the approximation of a random vector
-error induced by the approximation of a random vector 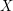 by a vector (quantized version) taking a finite number
by a vector (quantized version) taking a finite number  of values. For
of values. For 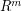 -valued random vectors the theory and practice is quite well established and in particular, the asymptotics as
-valued random vectors the theory and practice is quite well established and in particular, the asymptotics as 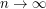 of the resulting minimal quantization error for nonsingular distributions is well known: it behaves like
of the resulting minimal quantization error for nonsingular distributions is well known: it behaves like 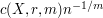 . This paper is a transposition of this problem to random vectors in an infinite dimensional Hilbert space and in particular, to stochastic processes
. This paper is a transposition of this problem to random vectors in an infinite dimensional Hilbert space and in particular, to stochastic processes ![$ (X_t)_{t \in [0,1]} $](/sites/default/files/tex/98bd9f498338ce7efbb2ccf5f20055f0f356310b.png) viewed as
viewed as ![$ L^2([0,1],dt) $](/sites/default/files/tex/97f973def8ab85a3be243077f6b2b87c2b850600.png) -valued random vectors. For Gaussian vectors and the
-valued random vectors. For Gaussian vectors and the 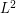 -error we present detailed results for stationary and optimal quantizers. We further establish a precise link between the rate problem and Shannon–Kolmogorov’s entropy of
-error we present detailed results for stationary and optimal quantizers. We further establish a precise link between the rate problem and Shannon–Kolmogorov’s entropy of 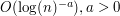 . They are obtained, for instance, for the fractional Brownian motion and the fractional Ornstein–Uhlenbeck process. The exponent a is closely related with the
. They are obtained, for instance, for the fractional Brownian motion and the fractional Ornstein–Uhlenbeck process. The exponent a is closely related with the 