| Title | Quantization of probability distributions under norm-based distortion measures II: Self-similar distributions |
| Publication Type | Journal Article |
| Year of Publication | 2006 |
| Authors | Sylvain Delattre, Siegfried Graf, Harald Luschgy, and Gilles Pagès |
| Journal | Journal of Mathematical Analysis and Applications |
| Volume | 318 |
| Pagination | 507 - 516 |
| ISSN | 0022-247X |
| Keywords | Point density measure |
| Abstract | For a probability measure |

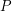 on
on 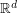 and
and 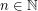 consider
consider 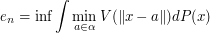 where the infimum is taken over all subsets
where the infimum is taken over all subsets  of
of 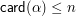 and
and 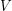 is a nondecreasing function. Under certain conditions on
is a nondecreasing function. Under certain conditions on  -asymptotics of
-asymptotics of 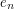 for nonsingular and for (singular) self-similar distributions
for nonsingular and for (singular) self-similar distributions 