Home » Publications

Optimal quantizers for Radon random vectors in a Banach space

TitleOptimal quantizers for Radon random vectors in a Banach space
Publication TypeJournal Article
Year of Publication2007
AuthorsSiegfried Graf, Harald Luschgy, and Gilles Pagès
JournalJ. Approx. Theory
Volume144
Pagination27–53
ISSN0021-9045
Abstract

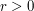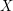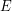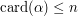For every integer $ n $ and evrery positive real number $ r \superior 0 $ and a Radon random vector $ X $ with values in a Banach space $ E $, let $ e_{n,r}(X,E) = \inf{\left(E\left[\min\limits_{a \in \alpha} \| X-a \|^r \right]^{1/r}\right)} $, where the infimum is taken over all subsets $ \alpha $ of $ E $ with $ \textrm{card}(\alpha) \leq n $ ($ n $-quantizers). 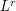We investigate the existence of optimal $ n $-quantizers for this $ L^r $-quantization problem, derive their stationarity properties and establish for 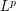$ L^p $-spaces $ E $ the pathwise regularity of stationary quantizers.