We present an approximation method for discrete time nonlinear filtering in view of solving dynamic optimization problems under partial information. The method is based on quantization of the Markov pair process filter-observation 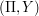 and is such that, at each time step k and for a given size and is such that, at each time step k and for a given size 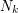 of the quantization grid in period of the quantization grid in period 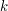 , this grid is chosen to minimize a suitable quantization error. The algorithm is based on a stochastic gradient descent combined with Monte-Carlo simulations of , this grid is chosen to minimize a suitable quantization error. The algorithm is based on a stochastic gradient descent combined with Monte-Carlo simulations of  . Convergence results are given and applications to optimal stopping under partial observation are discussed. Numerical results are presented for a particular stopping problem : American option pricing with unobservable volatility. . Convergence results are given and applications to optimal stopping under partial observation are discussed. Numerical results are presented for a particular stopping problem : American option pricing with unobservable volatility. | 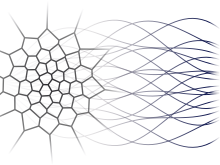
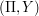 and is such that, at each time step k and for a given size
and is such that, at each time step k and for a given size 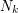 of the quantization grid in period
of the quantization grid in period 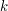 , this grid is chosen to minimize a suitable quantization error. The algorithm is based on a stochastic gradient descent combined with Monte-Carlo simulations of
, this grid is chosen to minimize a suitable quantization error. The algorithm is based on a stochastic gradient descent combined with Monte-Carlo simulations of 