| Title | Asymptotically optimal quantization schemes for Gaussian processes |
| Publication Type | Journal Article |
| Year of Publication | 2010 |
| Authors | Harald Luschgy, Gilles Pagès, and Benedikt Wilbertz |
| Journal | ESAIM: PS |
| Volume | 14 |
| Pagination | 93 - 116 |
| Keywords | Brownian motion, functional quantization, Gaussian process, optimal quantizer, Riemann-Liouville process |
| Abstract | We describe quantization designs which lead to asymptotically and order optimal functional quantizers. Regular variation of the eigenvalues of the covariance operator plays a crucial role to achieve these rates. For the development of a constructive quantization scheme we rely on the knowledge of the eigenvectors of the covariance operator in order to transform the problem into a finite dimensional quantization problem of normal distributions. Furthermore we derive a high-resolution formula for the |
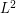 -quantization errors of Riemann-Liouville processes.
-quantization errors of Riemann-Liouville processes.