| Title | On the link between small ball probabilities and the quantization problem for Gaussian measures on Banach spaces |
| Publication Type | Journal Article |
| Year of Publication | 2003 |
| Authors | Steffen Dereich, F. Fehringer, A. Matoussi, and M. Scheutzow |
| Journal | Journal of Theoretical Probability |
| Volume | 16(1) |
| Keywords | Gaussian process, High-resolution quantization, isoperimetric inequality., small ball probability |
| Abstract | Let m be a centered Gaussian measure on a separable Banach space |
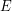 and
and 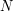 a positive integer. We study the asymptotics as
a positive integer. We study the asymptotics as 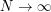 of the quantization error, i.e., the infimum over all subsets
of the quantization error, i.e., the infimum over all subsets  of
of  to the closest point in the set
to the closest point in the set  . Under slight conditions on the regular variation of the small ball function, we get upper and lower bounds of the deterministic and random quantization error and are able to show that both are of the same order. Our conditions are typically satisfied in case the Banach space is infinite dimensional.
. Under slight conditions on the regular variation of the small ball function, we get upper and lower bounds of the deterministic and random quantization error and are able to show that both are of the same order. Our conditions are typically satisfied in case the Banach space is infinite dimensional.