Home ยป Publications

Universal $L^s$-rate-optimality of $L^r$-optimal quantizers by dilatation and contraction

TitleUniversal $L^s$-rate-optimality of $L^r$-optimal quantizers by dilatation and contraction
Publication TypeJournal Article
Year of Publication2009
AuthorsAbass Sagna
JournalESAIM: Probability and Statistics
Volume13
Pagination218-246
Keywordsdilatation, empirical measure theorem, Lloyd algorithm, rate-optimal quantizers
Abstract

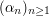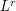We investigate in this paper the properties of some dilatations or contractions of a sequence $ (\alpha _{n})_{n \ge 1} $ of $ L^r $-optimal quantizers of an 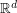$ \mathbb{R}^d $-valued random vector 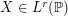$ X \in L^r(\mathbb{P}) $ defined in the probability space 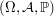$ (\Omega ,\mathcal{A},\mathbb{P}) $ with distribution 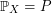$ \mathbb{P}_{X} = P $. 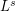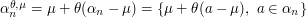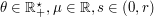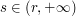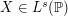To be precise, we investigate the $ L^s $-quantization rate of sequences $ \alpha _n^{\theta ,\mu } = \mu + \theta (\alpha _n-\mu )=\lbrace \mu + \theta (a-\mu ), \ a \in \alpha _n \rbrace $ when $ \theta \in \mathbb{R}_{+}^{\star }, \mu \in \mathbb{R}, s \in (0,r) $ or $ s \in (r,+\infty ) $ and $ X \in L^s(\mathbb{P}) $. 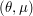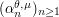We show that for a wide family of distributions, one may always find parameters $ (\theta ,\mu ) $ such that $ (\alpha _n^{\theta ,\mu })_{n \ge 1} $ is $ L^s $-rate-optimal. 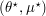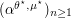For the gaussian and the exponential distributions we show the existence of a couple $ (\theta ^{\star }, \mu ^{\star }) $ such that $ (\alpha ^{\theta ^{\star },\mu ^{\star }})_{n \ge 1} $ also satisfies the so-called 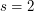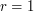$ L^s $-empirical measure theorem. Our conjecture, confirmed by numerical experiments, is that such sequences are asymptotically $ L^s $-optimal. In both cases the sequence $ (\alpha ^{\theta ^{\star },\mu ^{\star }})_{n \ge 1} $ is incredibly close to $ L^s $-optimality. However we show (see Rem. 5.4) that this last sequence is not $ L^s $-optimal (e.g. when $ s = 2 $, $ r = 1 $) for the exponential distribution.