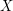 is a bi-measurable
is a bi-measurable 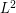 stochastic process on
stochastic process on ![$ [0,T] $](/sites/default/files/tex/b9baa7710b108fe1c29bd70224f83e1ccc813636.png) , it can be considered as a random variable valued in the Hilbert space
, it can be considered as a random variable valued in the Hilbert space ![$ H = L^2([0,T]) $](/sites/default/files/tex/00877b76d19e19f0137f4e585fcc7210328d864d.png) .
.
In [1], it is shown that in the Gaussian case, if the covariance function 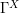 is continuous, linear subspaces
is continuous, linear subspaces 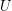 of
of 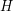 spanned by
spanned by 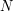 -stationary codebooks correspond to principal components of
-stationary codebooks correspond to principal components of 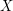 , in other words, are spanned by eigenvectors of the covariance operator of
, in other words, are spanned by eigenvectors of the covariance operator of 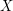 .
.
Thus, the quantization consists first in exploiting the Karhunen-Loève decomposition. The discretization consists in truncating the decomposition at a fixed order 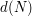 and to quantize the
and to quantize the 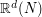 -value Gaussian vector constituted of the
-value Gaussian vector constituted of the 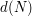 first coordinates of the process on its Karhunen-Loève decomposition.
first coordinates of the process on its Karhunen-Loève decomposition.
To reach optimal quantization, one has both to determine the optimal rank of truncation 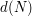 (the quantization dimension) and to determine the optimal
(the quantization dimension) and to determine the optimal 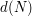 -dimensional Gaussian quantizer corresponding to the first coordinates.
-dimensional Gaussian quantizer corresponding to the first coordinates.
Formally, if 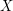 is a bi-measurable
is a bi-measurable ![$ L^2([0,T]) $](/sites/default/files/tex/5dac4e73536ca47ece3e71da86eb09c8f7544b45.png) Gaussian process, with a continuous covariance function, its Karhunen-Loève expansion
Gaussian process, with a continuous covariance function, its Karhunen-Loève expansion 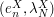 writes:
writes:
![$\displaystyle X = \sum\limits_{k=1}^\infty \xi_n^X e_n^X \ \in L^2(\Omega \times [0,T]), $](/sites/default/files/tex/e85101a4db542dddfa6bdadc8e23e77231cdcf15.png)
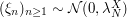 is a sequence of independent Gaussian random variables.
is a sequence of independent Gaussian random variables.
The terms of the Karhunen-Loève decomposition are explicit for classical Gaussian processes (the standard Brownian motion, the Brownian bridge and the Ornstein-Uhlenbeck process).
- The Karhunen-Loève decomposition of the standard Brownian motion
 on
on ![$ [0,T] $](/sites/default/files/tex/b9baa7710b108fe1c29bd70224f83e1ccc813636.png) is:
is:
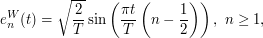
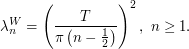
- The Karhunen-Loève decomposition of the standard Brownian bridge
 on
on ![$ [0,T] $](/sites/default/files/tex/b9baa7710b108fe1c29bd70224f83e1ccc813636.png) is:
is:
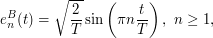
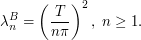
In this case, the 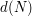 -dimensional random vector to be quantized is a Gaussian vector with diagonal variance-covariance matrix
-dimensional random vector to be quantized is a Gaussian vector with diagonal variance-covariance matrix 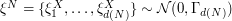 with
with 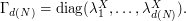
Optimal quantization of the Brownian motion
The compressed folder brownian_optimal_grids.zip contains optimal quantization grids of the standard Brownian motion.
To get optimal quantization, the point now is to quantize the finite-dimensional Gaussian vector 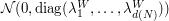 optimally.
optimally.
Hence, the method is the same as for the standard distribution except that the simulated Gaussian vector is not standard. For a given size 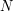 , all possible dimensions are tested, and the one that yields the smaller quadratic distortion (
, all possible dimensions are tested, and the one that yields the smaller quadratic distortion (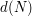 ) is kept.
) is kept.
For a given size 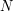 , the text files are organized as follows. It presents in the form of a matrix
, the text files are organized as follows. It presents in the form of a matrix 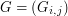 with
with 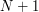 rows and
rows and 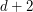 columns.
columns.
- On row
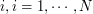 : Element
: Element 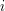 of the grid and its companion parameters. Consider
of the grid and its companion parameters. Consider 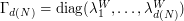
![$$
G_{i,1} = \left(\textrm{weight of the Voronoi cell of element } i \right)= \mathbb{P}[ \mathcal{N}(0,\Gamma_{d(N)}) \in C_i(G) ].
$$](/sites/default/files/tex/5b14e454943caa6f8a85b1a4c489190f14a2a4d7.png)
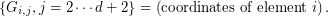

- On last row
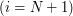 :
:
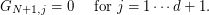

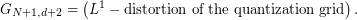
In particular we can verify that
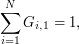 |
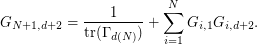 |
For further details and further reading, let us refer to [1].
Product quantization of the Brownian motion and the Brownian bridge
An other way to get a good quantizer of a Gaussian process is Product Quantization. In practice, 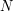 being settled, one determines the truncation threshold
being settled, one determines the truncation threshold 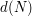 of the decomposition and then,
of the decomposition and then, 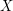 is approximated by
is approximated by 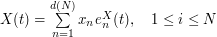 where
where 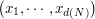 is a quantizer of the
is a quantizer of the 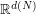 -valued random vector
-valued random vector 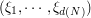 .
.
The product quantization consists in choosing the quantizer 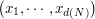 of
of 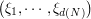 as a Cartesian product of one dimensional quantization grids.
as a Cartesian product of one dimensional quantization grids.
Thus, one replaces 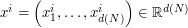 by
by 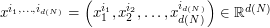 where
where 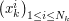 ,
, 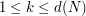 are optimized quantizers of the
are optimized quantizers of the 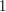 -dimensional Gaussian distribution, of size
-dimensional Gaussian distribution, of size 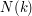 , and where the values
, and where the values 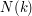 are such that
are such that 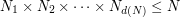 . A database of optimal quadratic quantizers of the standard Gaussian distribution is available here.
. A database of optimal quadratic quantizers of the standard Gaussian distribution is available here.
After all, one has for a settled integer 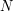 to determine among all its possible product decomposition the one that minimizes the distortion error.
to determine among all its possible product decomposition the one that minimizes the distortion error.
In article [2], the optimal product decompositions are used to compute Asian option prices in a stochastic volatility model.
Data to download:
|
|
|
The text file RECORD_QF.TXT contains optimal product decompositions for the standard Brownian motion of size 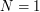 to
to 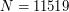 .
.
The text file RECORD_QF_BB.TXT contains optimal product decompositions for the standard Brownian bridge of size 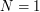 to
to 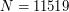 .
.
The both cases two first columns give, for a number 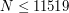 , the value of the distortion of the optimal product quantization.
, the value of the distortion of the optimal product quantization.
The following columns give the size 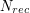 of the best product quantizer for a maximum number of points of
of the best product quantizer for a maximum number of points of 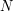 , and the corresponding distortion. At least, the corresponding optimal product decomposition is given.
, and the corresponding distortion. At least, the corresponding optimal product decomposition is given.

