Introduction
The following stochastic volatility model for the stock price dynamic in an incomplete market was introduced by Heston in 1993 [1]. Under a Risk-Neutral probability 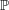 , it writes:
, it writes:
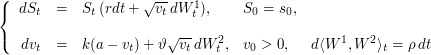 |
where ![$ \rho \in [-1,1] $](/sites/default/files/tex/91ef26f870ae28b2f658c46755bb216d064310f5.png) and where
and where 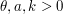 are such that
are such that 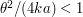 . Here
. Here 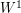 and
and 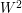 are two standard Brownian motions under the probability measure
are two standard Brownian motions under the probability measure 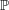 . Consider the Asian Call option of maturity
. Consider the Asian Call option of maturity 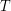 and strike
and strike 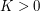 for which there is no explicit formula:
for which there is no explicit formula:
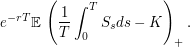 |
As a first step, we project 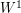 onto
onto 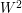 , so that
, so that 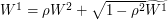 where
where 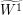 is a standard Brownian motion independent of
is a standard Brownian motion independent of 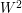 under the probability measure
under the probability measure 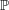 . Then
. Then 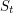 writes
writes
| TeX Embedding failed! |
where  .
.
Consider now 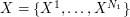 and
and 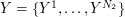 two functional quantizers of the Brownian motion.
two functional quantizers of the Brownian motion.
| TeX Embedding failed! |
where tabs 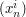 andt
andt 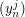 are available here.
are available here.
For 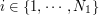 and
and 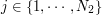 , we numerically solve the following ordinary differential equations.
, we numerically solve the following ordinary differential equations.
| TeX Embedding failed! |
(Here, we used a Runge Kutta IV method.) The option price is now approximated by
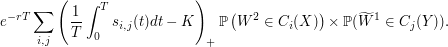 |
Numerical test
Here, we propose a method to compute the Asian call option price based on the functional quantization of the Brownian motion as described in article [2] (section 8).
Here 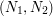 et
et 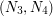 are the sizes of optimal functional quantizers of the standard Brownian motion (
are the sizes of optimal functional quantizers of the standard Brownian motion (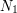 "points", i.e. paths, for
"points", i.e. paths, for 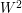 et
et 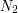 for
for 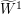 ). Parameter
). Parameter  stands for the number of time-steps used to solve the ordinary differential equation written above. (We used a fourth order Runge Kutta scheme). Each grid couple yields a price approximation. The final result is a Romberg extrapolation between both prices, based on a
stands for the number of time-steps used to solve the ordinary differential equation written above. (We used a fourth order Runge Kutta scheme). Each grid couple yields a price approximation. The final result is a Romberg extrapolation between both prices, based on a 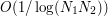 rate of convergence for the quadrature error.
rate of convergence for the quadrature error.
The following program was developed with the C programming language, and interfaced with Ruby. You can contact the authors for the source code.
The site team would like to thank David Delavennat (CNRS ingeneer at LAMA-UMR 8050 Univ. MLV - Paris 12 from 2003 to 2007) for his advices on the Ruby interface.
References
- "A closed-form solution for options with stochastic volatility with an application to bond and currency options", The Review of Financial Studies , vol. 6, issue 2, pp. 327 - 343, 1993.
- "Functional quantization for numerics with an application to option pricing", Monte Carlo Methods and Appl., vol. 11, no. 11, pp. 407-446, 2005.

