We propose a new method based on evolutionary optimization for obtaining an optimal 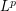 -quantizer of a multidimensional random variable. First, we remind briefly the main results about quantization. Then, we present the classical gradient-based approach (this approach is well detailed in [2] and [7] for -quantizer of a multidimensional random variable. First, we remind briefly the main results about quantization. Then, we present the classical gradient-based approach (this approach is well detailed in [2] and [7] for 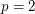 ) used up to now to find a “local” optimal ) used up to now to find a “local” optimal 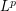 -quantizer. Then, we give an algorithm that permits to deal with the problem in the evolutionary optimization framework and illustrate a numerical comparison between the proposed method and the stochastic gradient method. Finally, a numerical application to option pricing in finance is provided. -quantizer. Then, we give an algorithm that permits to deal with the problem in the evolutionary optimization framework and illustrate a numerical comparison between the proposed method and the stochastic gradient method. Finally, a numerical application to option pricing in finance is provided. | 
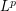 -quantizer of a multidimensional random variable. First, we remind briefly the main results about quantization. Then, we present the classical gradient-based approach (this approach is well detailed in [2] and [7] for
-quantizer of a multidimensional random variable. First, we remind briefly the main results about quantization. Then, we present the classical gradient-based approach (this approach is well detailed in [2] and [7] for 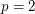 ) used up to now to find a “local” optimal
) used up to now to find a “local” optimal 