We quantize a multidimensional SDE (in the Stratonovich sense) by solving the related system of ODE’s in which the 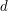 -dimensional Brownian motion has been replaced by the components of functional stationary quantizers. We make a connection with rough path theory to show that the solutions of the quantized solutions of the ODE converge toward the solution of the SDE. On our way to this result we provide convergence rates of optimal quantizations toward the Brownian motion for -dimensional Brownian motion has been replaced by the components of functional stationary quantizers. We make a connection with rough path theory to show that the solutions of the quantized solutions of the ODE converge toward the solution of the SDE. On our way to this result we provide convergence rates of optimal quantizations toward the Brownian motion for  -Hölder distance, -Hölder distance, 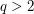 , in , in 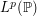 . . | 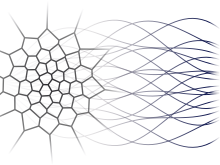
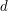 -dimensional Brownian motion has been replaced by the components of functional stationary quantizers. We make a connection with rough path theory to show that the solutions of the quantized solutions of the ODE converge toward the solution of the SDE. On our way to this result we provide convergence rates of optimal quantizations toward the Brownian motion for
-dimensional Brownian motion has been replaced by the components of functional stationary quantizers. We make a connection with rough path theory to show that the solutions of the quantized solutions of the ODE converge toward the solution of the SDE. On our way to this result we provide convergence rates of optimal quantizations toward the Brownian motion for  -Hölder distance,
-Hölder distance, 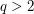 , in
, in 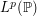 .
.